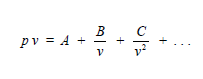ILMUWAN FISIKA : JAMES PRESCOTT JOULE

James Prescott Joule (lahir di Salford, Inggris, 24 Desember 1818 – meninggal di Greater Manchester, Inggris, 11 Oktober 1889 pada umur 70 tahun) ialah seorang ilmuwan Inggris. Ia dikenal sebagai perumus Hukum Kekekalan Energi, yang berbunyi,

“

Energi tidak dapat diciptakan ataupun dimusnahkan.

”

Ia adalah seorang ilmuwan Inggris yang berminat pada fisika. Dengan percobaan, ia berhasil membuktkan bahwa panas (kalori) tak lain adalah suatu bentuk energi. Dengan demikian ia berhasil mematahkan teori kalorik, teori yang menyatakan panas sebagai zat alir.

Salah satu satuan energi—Joule—dinamai atasnya.

Termodinamika dalam keseharian

Percobaan Perubahan Tekanan

Ilmu Termodinamika menyanggah Evolusi

Hukum II Termodinamika yg dianggap sebagai salah satu hukum dasar ilmu fisika menyatakan bahwa pada kondisi normal semua sistem yg dibiarkan tanpa gangguan cenderung menjadi tak teratur terurai dan rusak sejalan dgn waktu. Seluruh benda hidup atau mati akan aus rusak lapuk terurai dan hancur. Akhir seperti ini mutlak akan dihadapi semua makhluk dgn caranya masing-masing dan menurut hukum ini proses yg tak terelakkan ini tidak dapat dibalikkan. Kita semua mengamati hal ini. Sebagai contoh jika Anda meninggalkan sebuah mobil di padang pasir Anda tidak akan menemukannya dalam keadaan lbh baik ketika Anda menegoknya beberapa tahun kemudian.

Prinsip Kerja Dispenser (Aplikasi Hk. Termodinamika 1)

VIDEO TERMODINAMIKA : Roket Air

VIDEO TERMODINAMIKA : Air mancur dalam Hk. Boyle

VIDEO TERMODINAMIKA : Aplikasi Hukum 2 Termodinamika : Air Conditioning (AC)

VIDEO TERMODINAMIKA : Termodinamika II Menurut Hukum Rudolf Clausius

VIDEO TERMODINAMIKA : Percobaan Termodinamika - The Bubble's Propeller

VIDEO TERMODINAMIKA : Pembuatan Mini AC

VIDEO TERMODINAMIK : Mesin Stirling Sederhana (Aplikasi Hukum Termodinamika)

ILMUWAN FISIKA TERMODINAMIKA : BENJAMIN THOMPSON

BENJAMIN THOMPSON

  Benjamin Thompson atau 'Count Rumford' (1753 – 1814) adalah penemu, ilmuwan, negarawan, dan tentara terkenal kelahiran Amerika. Benjamin Thompson dilahirkan di Woburn Utara, Massachusetts pada tanggal 26 Maret 1753 beragama Anglican. Ayahnya adalah seorang petani dan meninggal ketika Benjamin Thompson berumur 2 tahun. Ibunya, Ruth Simonds menikah lagi dengan Josiah Pierce pada bulan Maret 1976. Di masa kecilnya, Benjamin Thompson memiliki keterbatasan untuk sekolah sehingga dia lebih banyak belajar sendiri dan kemudian mendapat banyak pengetahuan dari teman dan kenalannya. 

  Pada usia 13 tahun, Benjamin Thompson mulai melakukan beberapa pekerjaan seperti menjadi juru tulis seorang importer, pedagang bahan kering dan kemudian magang di Doctor John Hay of Woburn, dimana Thompson mendapatkan banyak pengetahuan tentang ilmu medis. Bakat Thompson dalam bekerja dengan alat mekanis dan kemampuan bahasanya yang sangat baik membuat John Fowle, salah satu guru lulusan Harvard, membantunya untuk belajar dengan Professor John Winthrop di Harvard. 

   Pada tahun 1772, Thompson meninggalkan kota kelahirannya dan mengajar di salah satu sekolah di Bradford, Massachusetts sambil mempelajari ilmu pengetahuan pada Samuel Williams. Tidak beberapa kemudian, Thompson berpindah mengajar di Concord, New Hampshire atas undangan dari Timothy Walker. Di sana Benjamin Thompson hidup menumpang dan kemudian menikahi anak dari tuan rumahnya, Sarah Walker Rolfe yang merupakan janda kaya di daerah Concord. Istrinyalah yang memperkenalkan Thompson pada Gubernur Wentworth dari New Hampshire dan mengangkatnya menjadi mayor di New Hampshire Militia. 

  Pada saat revolusi Amerika meledak, Thompson diajak bergabung dengan Amerika untuk melawan Inggis karena dia memiliki hubungan penting dengan pemerintah Inggris namun dia menolak. Benjamin Thompson meninggalkan keluarganya di Amerika pada tahun 1974 dan bergabung dengan pemerintah Britania Raya (Inggris) sebagai penasihat Jenderal Thomas Gage. Pada tahun 1776, Thompson bekerja sebagai juru tulis di Sekretariat Negara kemudian jabatannya terus naik menjadi Sekretaris Provinsi Georgia, dan pada tahun 1779 Benjamin Thompson menjadi salah satu anggota Royal Society. 

  Selain politik, dunia militer juga digeluti oleh Benjamin Thompson. Benjamin Thompson pernah menjabat sebagai letnan kolonel pasukan Britania Raya dan mendapatkan gelar kesatrian dari Raja George III. Pada tahun 1785, Benjamin Thompson bergabung bersama pasukan Austria untuk melawan Turki dan di sana dia berkenalan dengan Pangeran Maximillian dari Bavaria yang mengundangnya untuk tinggal Bavaria. Thompson tinggal di Bavaria selama beberapa tahun untuk memimpin pasukan Bavaria yang kurang mendapatkan perhatian dan penghidupan yang layak, kemudian membuat perubahan besar di daerah tersebut. 

 Para tentara diberi bayaran lebih tinggi, dibuatkan sarana rekreasi, dan diberikan pendidikan gratis baik untuk tentara maupun anak-anak mereka. Benjamin Thompson juga memberikan penghasilan kepada pengemis jalanan dengan mempekerjakan mereka untuk menjahit pakaian tentara Bavaria yang kurang layak pakai. Pada tahun 1971, Benjamin Thompson dianugerahi gelar Count of the Holy Roman Empire. 

  Di samping mengurusi masalah politik dan militer, Thompson juga aktif meneliti berbagai hal, terutama bidang Fisika. Sekitar tahun 1975, Benjamin Thompson meneliti tentang gaya pada bubuk mesiu dan membangun sistem sinyal kelautan yang baru bagi tentara Inggris. Kontribusinya yang terbesar pada dunia Fisika adalah pemikirannya tentang teori kalor. Pada akhir abad ke-18, teori kalori yang dipercaya adalah bahwa kalor merupakan fluida yang dapat mengalir ke dalam tubuh ketika dipanaskan dan mengalir keluar ketika didinginkan. 

 Saat meneliti tentang bubuk mesiu, Benjamin Thompson menemukan adanya penyimpangan atau anomali yang tidak dapat dijelaskan dengan teori kalori. Di dalam laporannya kepada Royal Society yang berjudul "An Experimental Enquiry concerning the Source of Heat excited by Friction" (1798), Benjamin Thompson mengajukan suatu teori baru yang menyatakan bahwa kerja mekanis akan menghasilkan kalor dan kalor tersebut merupakan suatu bentuk gerak. Teori tersebut berhasil memberikan penjelasan mengapa panas yang dihasilkan dari gesekan peluru meriam (bubuk mesiu) tidak akan pernah habis. Peristiwa itu tak dapat dijelaskan dengan teori kalori terdahulu. 

  Di dalam laporan tersebut terdapat perhitungan jumlah kuantitas kalor yang diproduksi oleh energi mekanis. Teori yang dikemukakan Thompson bertentangan dengan teori kalori yang terdahulu dan banyak orang pada saat itu yang tidak yakin dengan Thompson hingga James Maxwell mengemukakan teori kinetik kalor pada tahun 1871. Penemuan-penemuan Thompson lainnya adalah kompor, oven, ketel ganda, dan pakaian penahan panas, serta mengembangkan cerobong asap dan tungku perapian yang ada. 

  Pada tahun 1804, Thompson menetap di Paris dan menikah dengan Madame Lavoisier, janda seorang ahli kimia Perancis, Antoine Lavoisier. Pernikahan tersebut hanya bertahan beberapa tahun dan pada 1807 Benjamin Thompson pensiun dan menetap di desa Auteuil dekat Paris. Thompson menjadi anggota Institusi Nasional Perancis sebagai dan secara rutin berkontribusi dalam berbagai pertemuan dan debat ilmu pengetahuan. Penghargaan yang pernah diraihnya adalah Copley Medal. Setelah perceraiannya, Thompson dirawat oleh anak perempuannya hingga pada tanggal 21 Agustus 1814, Benjamin Thompson meninggal di Auteuil, Paris pada usia 61 tahun. Dibangun Monumen Benjamin Thompson di English Garden.

Sejarah Pengembangan Konsep Temuan

• Pada panas 

  Percobaannya pada meriam dan bahan peledak menyebabkan minat panas. Dia menemukan metode untuk mengukur panas spesifik dari padatan tapi kecewa bahwa Johan Wilcke telah prioritas. Thompson berikutnya menyelidiki isolasi sifat dari berbagai macam bahan termasuk bulu , wol dan bulu . Dia benar menghargai bahwa sifat isolasi dari bahan alami timbul dari kenyataan bahwa mereka menghambat konveksi dari udara . Dia kemudian membuat agak sembrono, dan tidak benar, kesimpulan bahwa udara dan, pada kenyataannya, semua gas , yang sempurna non- konduktor panas.

    Dia lebih jauh melihat ini sebagai bukti dari argumen dari desain , berpendapat bahwa ilahi takdir telah mengatur untuk bulu pada hewan sedemikian rupa untuk menjamin kenyamanan mereka.  Pada 1797, ia diperpanjang klaim tentang non-konduktivitas untuk cairan . Gagasan menyatakan keberatan cukup dari berdirinya ilmiah, John Dalton dan John Leslie terus terang membuat serangan khususnya. Instrumentasi jauh melebihi apa yang tersedia dalam hal akurasi dan presisi akan diperlukan untuk memverifikasi mengklaim Thompson. Sekali lagi, ia tampaknya telah dipengaruhi oleh nya teologis keyakinan dan kemungkinan bahwa ia ingin memberikan air dan takdir status istimewa dalam regulasi kehidupan manusia.

• setara Mekanik panas 

    Namun, karya ilmiah Rumford yang paling penting berlangsung di Munich , dan berpusat pada sifat panas , yang ia berpendapat di Sebuah Pertanyaan Eksperimental Tentang Sumber Heat yang terpesona oleh Gesekan (1798) bukanlah kalori dari kemudian-saat ini ilmiah berpikir tetapi suatu bentuk gerak . Rumford telah mengamati gesek panas yang dihasilkan oleh meriam membosankan di gudang senjata di Munich.Rumford per barel meriam terbenam dalam air dan mengatur alat membosankan khusus tumpul. Dia menunjukkan bahwa air dapat direbus dalam sekitar dua setengah jam dan bahwa pasokan panas gesekan itu tampaknya tak ada habisnya. Rumford mengkonfirmasikan bahwa tidak ada perubahan fisik yang terjadi dalam material meriam dengan membandingkan spesifik memanaskan material mesin pergi dan yang tersisa.

   Rumford berpendapat bahwa generasi yang tampaknya tidak terbatas panas sangat tidak sesuai dengan teori kalori.Dia berpendapat bahwa satu-satunya dikomunikasikan kepada barel itu gerakan. Rumford tidak berusaha untuk lebih mengukur panas yang dihasilkan atau untuk mengukur setara mekanik panas. Meskipun pekerjaan ini bertemu dengan resepsi bermusuhan, itu kemudian penting dalam membangun hukum kekekalan energi kemudian di abad ke-19. 

• perapian dan pot kopi  

   Thompson adalah penemu aktif dan produktif, mengembangkan perbaikan untuk cerobong asap dan perapian dan menciptakan ganda boiler , suatu rentang dapur , dan tetes kopi . perapian Rumford adalah cara yang jauh lebih efisien untuk memanaskan perapian sebuah kamar dari sebelumnya, dan menciptakan sensasi di London ketika ia memperkenalkan ide membatasi pembukaan cerobong untuk meningkatkan updraught. Dia dan para pekerjanya berubah perapian dengan menyisipkan ke dalam perapian batu bata untuk membuat dinding sisi siku dan menambahkan tercekik cerobong untuk meningkatkan kecepatan udara naik buang tersebut.

Tungku ciptaan Benjamin Thompson

    Ini secara efektif menghasilkan aliran udara streamline, sehingga semua asap akan naik ke cerobong daripada berlama-lama, masuk kamar dan sering tersedak penduduk. Hal ini juga memiliki efek meningkatkan efisiensi api, dan memberikan kontrol ekstra laju pembakaran bahan bakar, baik kayu atau batubara . Banyak rumah mode London telah diubah dengan petunjuk-Nya, dan menjadi bebas asap. Thompson menjadi selebriti ketika berita kesuksesannya menjadi luas.

  Karyanya juga sangat menguntungkan, dan banyak ditiru ketika ia menerbitkan analisisnya tentang cara bekerja cerobong asap. Dalam banyak hal, ia mirip dengan Benjamin Franklin , yang juga menciptakan jenis baru pemanasan kompor berdasarkan cara baru dalam mengontrol aliran udara ke dan melalui tungku .  Dia menciptakan percolating pot kopi berikut karya rintisannya dengan Bayern Angkatan Darat, di mana ia memperbaiki diet para prajurit serta pakaian mereka. 

Retensi panas adalah sesuatu dari motif utama , karena ia juga dikreditkan dengan penemuan pakaian termal.

• Cahaya dan fotometri 

    Rumford adalah orang yang fotometri , pengukuran cahaya. Dia membuat alat pengukur cahaya untuk pemotretan dan memperkenalkan lilin, pendahulu dari candela , sebagai unit intensitas cahaya . lilin standar adalah terbuat dari minyak ikan paus sperma, dengan spesifikasi kaku.Ia juga menerbitkan studi tentang "ilusi" atau warna komplementer subyektif, disebabkan oleh bayang-bayang yang diciptakan oleh dua lampu, satu putih dan satu berwarna; observasi ini dikutip dan digeneralisasikan oleh Michel-Eugène Chevreul sebagai hukum-Nya "kontras warna serentak" pada 1839. 

Penerapan Konsep Temuan

Konsep temuan Benjamin Thompson dapat digunakan dalamkompor, oven, ketel ganda, dan pakaian penahan panas, serta mengembangkan cerobong asap dan tungku perapian yang ada.

BRILLOUIN

TEORI BRILLOUIN

Teori mengenai sistem paramagnetik berikutnya adalah teori Brillouin (baca Briluan). Brillouin dengan menggunakan teori kuantum dan fisika statistik memperoleh persamaan keadaan sistem paramagnetik sebagai berikut.

Sistem Dielektrik

Sistem atau zat dielektrik secara keseluruhan mempunyai besaran-besaran polarisasi P, medan listrik luar dengan kuat medan listrik Є, dan temperatur T. Sistem atau zat dielektrik dapat digambarkan sebagai berikut.

Zat dielektrik, jika tidak dikenai medan listrik luar, maka atom atau molekulnya memiliki pusat muatan positif yaitu inti atom yang berimpit dengan pusat muatan negatifnya, yaitu elektron (perhatikan gambar.a). Jika zat dielektrik dikenai atau dimasukkan ke dalam medan listrik luar dengan kuat medan listrik Є, maka zat dielektrik akan terkena induksi (imbas) medan listrik. Karena terkena medan listrik luar, maka pusat muatan positif inti dan elektron atom tidak lagi berimpit, melainkan agak bergeser (tergeser), sehingga atom atau molekul menyerupai dipole listrik yang kecil sekali (perhatikan gambar b).

Ini berarti atom-atom zat dielektrik diarahkan oleh medan listrik luar. Peristiwa terarahnya atom-atom zat dielektrik ini dikenal sebagai peristiwa polarisasi.

Dengan peristiwa polarisasi, atom-atom zat dielektrik menjadi dipole listrik. Oleh karena itu, ada dua besaran zat dielektrik, yaitu: polarisasi (P) dan kaut medan listrik luar (Є) yang saling mempengaruhi; sehingga disebut sebagai variabel keadaan atau koordinat sistem dielektrik.

Bagaimana kalau temperatur zat dielektrik dinaikkan ? Jika temperatur zat dielektrik dinaikkan, maka getaran atom atau molekul zat dielektrik semakin hebat; sehingga arah positif dan negatifnya atom yang netral semakin acak. Karena semakin acak, maka kenaikan temperatur pada hakikatnya menentang terorientasinya muatan atom-atom zat dielektrik

Dengan ini jelas bahwa temperatur juga mempengaruhi polarisasi, sehingga temperatur juga merupakan variabel keadaan atau koordinat sistem dielektrik.

Bagaimana polarisasi P zat dielektrik, jika zat dielektrik dimasukkan dalam medan listrik luar dengan kuat medan listrik Є, dan temperatur T zat dielektrik dinaikkan ? Menurut hasil eksperimen, salah satu hubungan antara polarisasi P, kuat medan listrik Є, dan temperatur T ditunjukkan oleh persamaan berikut.

Dengan a dan b sebagai tetapan yang harganya ditentukan dengan eksperimen

Sistem Dawai Teregang

Semua bahan berubah bentuk karena pengaruh gaya. Ada bahan yang kembali ke bentuk aslinya bila gaya yang mempengaruhi dihilangkan, bahan yang seperti ini disebut bahan yang lenting sempurna. Ada pula bahan yang tetap berubah bentuknya walaupun gaya yang mempengaruhi dihilangkan, bahan yang seperti ini disebut bahan tidak lenting sempurna. Namun tidak boleh ada gaya yang melebihi kekuatan maksimum bahan.

Jika ada gaya yang melebihi kekuatan maksimum bahan, maka bahan akan putus, patah, atau retak. Batas ini disebut sebagai batas kelentingan bahan. Sifat-sifat kelentingan bahan dijelaskan dengan dua pengertian dasar, yaitu: stres dan strain.

Gambar a melukiskan sebuah batang baja A yang ditarik oleh dua gaya yang sama, ke kanan dan kekiri, yaitu: F. Karena kuatnya gaya tarik tersebut, maka batang baja akan mengecil dan berubah bentuknya menjadi batang B. Perubahan bentuk ini tetap, walaupun kedua gaya tarik dihilangkan.

Gambar b melukiskan sebuah batang baja A yang ditekan dengan gaya yang berlawanan sebesar F. Akibatnya batang baja A membesar dan memendek serta berubah bentuknya menjadi B. Perubahan bentuk ini tetap, walaupun gaya tekan dihilangkan.

Selaput Tipis

Selaput tipis (Thin Layer) juga merupakan sistem termodinamis. Contoh konkret selaput tipis antara lain:

a. bagian atas permukaan cairan dalam kesetimbangan dengan uapnya,

b. gelembung sabun atau selaput sabun yang teregang pada suatu kerangka yang terjadi dari dua permukaan selaput sabun dengan sedikit cairannya, dan

c. lapisan minyak di atas permukaan air.

Lapisan minyak di atas air mirip dengan membran yang teregang seperti gambar berikut.

Lapisan minyak menarik garis batas antara minyak dan air ke atas dengan gaya F yang tegak lurus garis batas serta lapisan air menarik garis batas antara minyak dan air ke bawah dengan gaya F’ yang tegak lurus garis batas. Dua gaya ini sama harganya hanya berlawanan arah. Gaya yang bekerja tegak lurus garis batas per satuan panjang disebut tegangan permukaan.

Keadaan selaput tipis ini diwakili oleh tiga koordinat sistem, yaitu:

a. tegangan permukaan (γ) dengan satuan N m ^{– 1}

b. luas selaput (A) dengan satuan m², dan

c. temperatur selasput tipis (T) dengan satuan kelvin (K).

Eksperimen menunjukkan, bahwa tegangan permukaan hanya fungsi temperatur saja. Oleh sebab itu, persamaan keadaan selaput tipis antara minyak (eka lapis) dan air dapat ditulis sebagai berikut.

dengan a = tetapan, γ = tegangan permukaan air yang diselimuti minyak eka lapis, γ_w = tegangan permukaan air bersih (murni), dan T = temperatur lapisan tipis.

Perbedaan (γ – γ_w) sering disebut tekanan permukaan. Selaput tipis seperti ini dapat dimampatkan dan dapat dimuaikan; sehingga sangat menarik jika dibahas dalam termodinamika. Selaput tipis antara minyak dan air jika diendapkan akan mempunyai sifat optis yang menarik; sehingga jika dibahas dalam optika fisis sangat menarik.

Sel Terbalikkan

Sel terbalikkan Daniell terdiri atas dua elektrode (tembaga / Cu dan seng / Zn) yang masing-masing dibenamkan dalam elektrolit yang berbeda (larutan Cu SO₄ jenuh dan larutan Zn SO₄ jenuh) yang dibatasi oleh dinding berpori-pori seperti gambar  berikut :

Eksperimen menunjukkan, bahwa elektrode Cu lebih positif dibanding dengan elektrode Zn; sehingga Cu disebut kutub positif dan Zn disebut kutub negatif. Jika sel Daniell tersebut dihubungkan dengan suatu potensiometer yang beda potensialnya lebih rendah sedikit dengan gaya gerak listrik (ggl) sel, maka arus listrik (pemindahan muatan positif) akan terjadi dari Cu ke Zn. Apabila hal ini terjadi, seng melarut, seng sulfat terbentuk, tembaga diendapkan, dan tembaga sulfatnya terpakai. Perubahan ini diungkapkan dengan reaksi kimia berikut :

Jika pemindahan muatan positif dibalik, dalam arti dari Zn ke Cu, maka akan terjadi: tembaga melarut, tembaga sulfat terbentuk, seng diendapkan, dan seng sulfatnya terpakai. Perubahan ini diungkapkan dengan reaksi kimia kebalikan dari reaksi diatas. 

Eksperimen menunjukkan, bahwa reaksi berlangsung dalam arah sebaliknya; sehingga sel Daniell disebut sel terbalikkan. Jika sel terbalikkan tidak menghasilkan gas dan bekerja pada tekanan udara luar yang tetap, maka variabel keadaan sistemnya hanya tiga, yaitu:

1. gaya gerak listriknya (ε) dengan satuan volt (V)

2. muatannya (Z) dengan satuan coulomb ( C), dan

3. temperaturnya (T) dengan satuan kelvin (K).

Sifat penting sel terbalikkan ialah perubahan kimia yang menyertai pemindahan muatan listrik dalam satu arah terjadi dengan harga yang sama dalam arah sebaliknya ketika jumlah muatan listrik yang sama dipindahkan dalam arah sebaliknya. Jadi, jika Δn mol seng lenyap dan Δn mol tembaga diendapkan, muatan sel berubah dari Z_i ke Z_f, dengan 

 Perlu diketahui, bahwa Z_i = muatan awal sel, Z_f = muatan akhir sel, j = valensi seng atau tembaga (dalam hal ini valensi seng = valensi tembaga = 2), dan N_F = tetapan Faraday = 96 500 C.

Namun eksperimen juga menunjukkan, bahwa ggl sel terbalikkan hanya fungsi temperatur saja. Dengan demikian, persamaan keadaan sistem sel terbalikkan adalah: 

dengan ε = ggl sembarang temperatur, ε₂₀ = ggl pada temperatur 20⁰C, t = temperatur dalam celcius, serta α, β, dan γ adalah tetapan yang bergantung pada bahan.

KOORDINAT INTENSIF DAN EKSTENSIF

Variabel keadaan sistem atau koordinat sistem ada dua macam, yaitu: koordinat intensif dan koordinat ekstensif. Koordinat intensif merupakan besaran yang nilainya (harganya) tidak bergantung pada ukuran sistem. Sedangkan kordinat ekstensif merupakan besaran yang nilainya ditentukan oleh ukuran sistem. Koordinat intensif dan ekstensif dijelaskan seperti tabel berikut :

sumber : HAMID, AHMAD ABU. 2007. DIKTAT PERKULIAHAN TERMODINAMIKA : KALOR DAN TERMODINAMIKA. YOGYAKARTA : FMIPA UNY.

SISTEM PERSAMAAN KEADAAN SISTEM

SISTEM DAN PERSAMAAN KEADAAN SISTEM

A. Keadaan Kesetimbangan Sistem dan Persamaan Keadaannya

Suatu sistem dapat berada dalam keadaan setimbang atau tidak setimbang. Ada empat keadaan setimbang suatu sistem. Keempat keadaan setimbang tersebut adalah:

1. keadaan setimbang mekanis

2. keadaan setimbang kimiawi (chemis / kemis)

3. keadaan setimbang termal / termis

4. keadaan setimbang termodinamis.

1. Keadaan Setimbang Mekanis

Suatu sistem dinyatakan berada dalam keadaan setimbang mekanis jika resultan gaya luar maupun resultan gaya dalamnya (gaya dachil) adalah nol. Ini berarti

Σ=0F

Dalam keadaan setimbang mekanis, suatu sistem dapat diam atau bergerak beraturan. Dalam arti bergerak lurus beraturan atau bergerak melingkar beraturan atau berotasi beraturan.

2. Keadaan Setimbang Kemis

Apabila suatu sistem

a. tidak mengalami perpindahan zat dari bagian satu ke bagian lainnya atau sistem tidak mengalami difusi

b. tidak terjadi reaksi kimiawi yang dapat mengubah jumlah partikel semula

c. tidak terjadi pelarutan

d. tidak terjadi kondensasi serta

e. komposisi dan konsentrasinya tetap,

                                                                                      

maka sistem itu berada dalam keadaan setimbang kemis (kimiawi). Ini berarti sistem dinyatakan setimbang kemis (kimiawi), jika sistem tidak berubah dan tetap berada dalam keadaan semula.

3. Keadaan Setimbang Termis

Apabila suatu sistem  :

a. koordinat makro maupun mikronya tidak berubah walaupun kontak termal dengan lingkungannya melalui dinding diatermik

b. harga koordinat makro maupun mikronya tidak berubah dengan perubahan waktu,

maka sistem berada dalam keadaan setimbang termis dengan lingkungannya. Oleh karena itu, suatu sistem disebut setimbang termis, jika harga koordinatnya tidak berubah dengan perubahan waktu.

4. Keadaan Setimbang Termodinamis

Apabila syarat-syarat kesetimbangan mekanis, kemis, dan termis terpenuhi, maka sistem berada dalam keadaan setimbang termodinamis. Dalam keadaan setimbang termodinamis, keadaan koordinat sistem maupun lingkungan sistem cenderung tidak berubah sepanjang masa. Jadi, pada dasarnya Termodinamika hanya mempelajari suatu sistem yang berada dalam kesetimbangan termodinamis.

Keadaan sistem yang setimbang termodinamis minimal ada dua, yaitu: sistem yang tertutup dan sistem yang terbuka. Suatu sistem dinyatakan tertutup, jika massa dan jumlah partikel sistem tetap. Ini berati, jumlah mol sistem yang tertutup selalu tetap.

Sebaliknya, sistem dinyatakan terbuka, jika massa dan jumlah partikel sistem berubah-ubah harganya. Ini berarti, jumlah mol sistem yang terbuka selalu berubah-ubah.

Dalam keadaan setimbang termodinamis, ternyata

a. setiap sistem tertutup dapat digambarkan oleh tiga koordinat sistem dari delapan koordinat yang dipunyainya

b. semua eksperimen menunjukkan bahwa antara ketiga koordinat itu terdapat hubungan berikut.

f (x, y, z) = 0

Ini berarti, dalam keadaan setimbang termodinamis, hanya dua diantara ketiga koordinat sistem yang merupakan variabel (ubahan) bebas. Pernyataan ini dapat dituliskan seperti persamaan berikut :

X = f(y,z)

Y = f(x,z)

Z = f(x,y)

Gas berada dalam silinder dengan koordinat sistem, G (energi bebas Gibbs dari gasa), p (tekanan gas), H (entalpi gas), S (entropi gas), U (energi dalam gas), V (volume gas), F (energi bebas Helmholtz), dan T (temperatur gas). Perhatikan tiga koordinatnya, misalnya: p, V, dan T. Andaikan V dan T ditentukan terlebih dulu secara bebas, misalnya: gas dimasukkan dalam silinder dengan volume V dan dipanasi sampai temperaturnya mencapai harga T, maka tekanan gas telah memiliki harga tertentu dan tidak dapat ditentukan secara bebas. Ini berarti:

P = F (V,T)

Andaikan p dan T ditentukan terlebih dulu secara bebas, misalnya: gas dimasukkan dalam silinder dengan tekanan p dan dipanasi sampai temperaturnya mencapai harga T, maka volume gas telah memiliki harga tertentu dan tidak dapat ditentukan secara bebas. Ini berarti

V = f (p,T)

Andaikan p dan V ditentukan terlebih dulu secara bebas, misalnya: gas dimasukkan dalam silinder dengan tekanan p dan ditekan sampai volumenya mencapai harga V, maka temperatur gas telah memiliki harga tertentu dan tidak dapat ditentukan secara bebas. Ini berarti:

T = f(p,V)

Dengan demikian, secara umum berlaku persamaan:

f(p,V.T) = 0

Persamaan diatas merupakan persamaan keadaan gas atau persamaan keadaan sistem yang berada dalam keadaan setimbang termodinamis.

B. Persamaan Keadaan Sistem

Ada beberapa sistem termodinamis (suatu sistem yang berada dalam keadaan setimbang termodinamis), yaitu:

1.Sistem Hidrostatis (Hidrostatik) atau Sistem Kemis (Kimiawi)

2. Sistem Paramagnetis (Paramagnetik).

3. Sistem Dielektris (Dielektrik).

4. Sistem Dawai yang Teregang.

5. Sistem Selaput Tipis.

6. Sistem Sel Listrik.

1. Sistem Hidrostatis

Sistem hidrostatis merupakan zat kimia yang tidak diperhatikan sifat kelistrikannya, kemagnetannya, elastisitasnya, dan sifat tegangan permukaannnya. Sistem hidrostatis ada dua, yaitu: zat murni dan zat tak murni. Contoh sistem hidrostatis adalah: gas, cairan, atau padatan.

Sistem hidrostatis disebut zat murni apabila terdiri atas satu senyawa kimia saja dan berada dalam keadaan setimbang termodinamis. Misalnya: Es (H₂O), Air (H₂O), Uap Air (H₂O), Karbondioksida (CO₂), Hidrogen (H₂), Nitrogen (N₂), atau Oksigen (O₂). Karbondioksida, hidrogen, nitrogen, dan oksigen dapat berada dalam wujud padatan, gas, maupun cairan.

Sistem hidrostatis disebut zat tak murni apabila terdiri atas campuran zat murni yang berada dalam keadaan setimbang termodinamis. Misalnya: udara yang terdiri dari campuran oksigen, nitrogen, uap air, dan karbondioksida. Dalam udara masih ada beberapa jenis gas lagi, namun jumlahnya sedikit sekali, misalnya gas argon, helium, neon, dan gas kripton.

Persamaan keadaan sistem hidrostatis dinyatakan dalam fungsi

f(p,V.T) = 0

a. Gas Ideal, dengan persamaan keadaan: p V = n R T

b. Gas Clausius, dengan persamaan kedaan: p (v – b) = R T

c. Gas van der Waals, dengan persamaan keadaan 

Dalam bentuk lain persamaan keadaan gas van der Waals dapat ditulis sebagai berikut.

p v² – (p b + R T) v² + a v – a b = 0

d. Persamaan keadaan gas real sebagai berikut.

 A, B, C, dan seterusnya disebut sebagai koefisien virial yang merupakan fungsi temperatur. Karena persamaan 3.8.b sama dengan persamaan 3.9, maka diperoleh:

A = R T, B = R T b, C = R T b², demikian selanjutnya

2. Sistem Paramagnetik

Sistem paramagnetik merupakan gas, cairan, padatan, atau campuran dari dua atau tiga wujud tersebut yang memiliki kuat medan magnet luar yang disebut induksi magnetik (B) yang mempengaruhi kemagnetan atom-atom atau magnetisasi (M). Sedangkan temperatur sistem paramagnetik mempengaruhi orientasi atom-atom sistem paramagnetik dan orientasi atom-atom ini akhirnya mempengaruhi magnetisasi.

Jadi sistem paramagnetik minimal mempunyai tiga koordinat sistem, yaitu: induksi magnetik luar (B), Magnetisasi (M), dan temperatur sistem paramagnetik (T). Sedangkan contoh sistem paramagnetik misalnya: Aluminum (Al), Calcium (Ca), Magnesium (Mg), dan Chromium (Cr).

Untuk jelasnya, ditinjau sebuah kristal Mg yang memiliki banyak atom, misalnya sebanyak m buah atom. Andaikan kristal ini dibiarkan begitu saja, maka kristal tetap dalam kondisi netral. Jika dipandang dari segi kemagnetannya, atom-atom Mg merupakan momen atau dipol magnetik (μ_i)) yang tertentu, sehingga dipol magnetik totalnya adalah:

Namun, karena arah dipol magnetik berbeda-beda (berorientasi secara acak) sedemikian rupa, sehingga magnetisasinya tidak ada atau sama dengan nol.

Atom-atom tidak terlihat mata, maka atom-atom yang bersifat magnet atau dipol magnetik ini merupakan magnet-magnet kecil sekali yang disebut magnet elementer. Karena arah magnet elementer berbeda-beda sedemikian rupa, sehingga kemagnetan kristal Mg juga tidak tampak atau kemagnetannya sama dengan nol, sehingga magnetisasinya juga sama dengan nol.

Pada hakikatnya momen magnetik atau dipol magnetik bersumber pada elektron yang mengelilingi inti dalam kulit atau sub kulit yang tidak penuh seluruhnya. Momen magnetik atom dinyatakan dalam satuan yang disebut sebagai magneton Bohr, yaitu:

μ_B ≈ 9 x 10 ^{– 24} A m²

Andaikan sistem paramagnetik yang berupa kristal Mg diperlakukan, misalnya diberi medan magnet luar yang kuat dengan induksi magnetik B, maka dipol magnetik atau magnet elementer arahnya akan terorientasi searah dengan medan magnet luar. Dengan demikian, sistem paramagnetik memiliki suatu besaran atau koordinat yang menyatakan kuat medan magnet luar yang disebut induksi magnetik B.

Tanpa medan magnet luar, sepotong kristal paramagnetik tidak memiliki apa yang dinamakan kemagnetan atau magnetisasi M, karena masing-masing magnet elementer atau dipol magnetik berorientasi acak. Karena ada medan magnet luar, maka magnet elementer atau dipol magnetik terorientasi searah dengan arah medan magnet luar. Boleh dinyatakan, magnet-magnet elementer atau dipol magnetik akan berusaha menyejajarkan (menjajarkan) diri dengan medan magnet luar. Dengan demikian magnetisasi M merupakan koordinat kedua sistem paramagnetik.

Koordinat ketiga sistem paramagnetik adalah temperatur (T). Mengapa demikian ? Karena penyejajaran (penjajaran) magnet elementer atau dipol magnetik (μ_i) oleh kuat medan magnet luar dengan induksi magnetik B ditentang oleh temperatur (T). Maksudnya, karena atom-atom dalam suatu kristal senantiasa bergetar, sedangkan kenaikan temperatur menyebabkan getaran semakin hebat, maka semakin tinggi temperatur semakin acak orientasi magnet elementer atau dipol magnetiknya, sehingga magnetisasinya (M) semakin kecil.

3. Teori Langevin dan Teori Brillouin

Perhatikan 2 gambar dibawah. Gambar pertama menunjukkan lukisan sebuah sistem paramagnetik atau sebuah kristal Mg dengan magnet elementer atau dipol magnetik (μ_i) yang arahnya acak tak keruan. Akibatnya apa ? Akibatnya kristal Mg tidak memiliki kemagnetan atau magnetisasi (M). Dengan demikian dapat dituliskan:

Jika magnetisasi didefinisikan sebagai dipol magnetik total per satuan volume, maka dapat dituliskan persamaan magnetisasi sebagai berikut.

Gambar kedua melukiskan sebuah kristal Mg yang berada dalam medan magnet luar dengan induksi magnetik B. Akibatnya apa ? Akibatnya, magnet elementer atau dipol magnetik terorientasi searah dengan arah kuat medan magnet luar, sehingga μ ≠ 0 dan 

Berapa energi sistem paramagnetik ? Energi sistem paramagnetik E menggambarkan interaksi antara induksi magnetik kuat medan magnet luar B dan induksi magnetik total magnet elementer atau dipol magnetik μ. Energi sistem paramagnetik E didefinisikan sebagai minus perkalian skalar μ dan B yang dapat ditulis sebagai berikut.

Pada saat B sejajar dan searah dengan μ, maka sudut θ = 0⁰, sehingga cos θ = 1 dan energi sistem paramagnetik dapat ditulis sebagai E = - μ B yang sering ditulis sebagai E_paralel = E_par = - μ B. Pada saat B sejajar dan berlawanan arah dengan μ, maka sudut θ = 180⁰, sehingga cos θ = - 1 dan energi sistem paramagnetik dapat ditulis sebagai E = + μ B yang sering ditulis sebagai E_{anti paralel} = E_ap = + μ B. Pada saat B tegak lurus dengan μ, maka sudut θ = 90⁰, sehingga cos θ = 0 dan energi sistem paramagnetik E = 0 yang sering ditulis sebagai E_┴ = 0. Jika hasil ini digambar, diperoleh gambar berikut :

Teori mengenai magnetisasi sistem paramagnetik telah dikemukakan satu abad yang lalu. Teori yang pertama dikemukakan oleh Langevin (baca Longevan) pada tahun 1905 yang menghasilkan persamaan keadaan berikut.

dengan n adalah jumlah dipol magnetik (N) per satuan volume (V) dan μ adalah dipol magnetik total dalam kristal atau sistem paramagnetik

dengan :

B = induksi magnetik dari kuat medan magnet luar

k = konstante Boltzmann = 1,3806 x 10 ^–23 J K ^–1

T = temperatur sistem paramagnetik

yang dikenal sebagai fungsi Langevin.

Dengan mensubstitusikan persamaan diatas, maka diperoleh :

Jika dihitung harga limit dari persamaan 3.19 pada dua kasus yang ekstrem, yaitu:

a.apabila kuat medan magnet luar sangat kuat dan temperatur

sistem paramagnetik sangat rendah, maka harga sangat besar

b. apabila kuat medan magnet luar sangat lemah dan temperatur sistem paramagnetik sangat tinggi, maka harga sangat kecil

Ketika x >> 1, maka coth x ≈ 1 dan dapat diabaikan, sehingga diperoleh persamaan: x1

M = μn

Persamaan tersebut menunjukkan, bahwa magnetisasi M mengalami kejenuhan sebagai hasil apabila semua molekul / atom-atom / magnet elementer / dipol magnetik sejajar dengan medan magnet luar.

Pada kuat medan magnet luar yang sangat kecil dan temperatur sistem paramagnetik sangat besar, maka x << 1 dan kita dapat menggunakan pendekatan untuk coth pada sebuah sudut yang kecil, sehingga diperoleh persamaan

maka didapat 

Dengan :

C = konstante Curie =  = 0,376 cm³ K mole^–1 dan persamaan ini  disebut sebagai hukum Curie.

Grafik fungsi Langevin dapat dilukiskan seperti gambar berikut

sumber : HAMID, AHMAD ABU. 2007. DIKTAT PERKULIAHAN TERMODINAMIKA : KALOR DAN TERMODINAMIKA. YOGYAKARTA : FMIPA UNY.